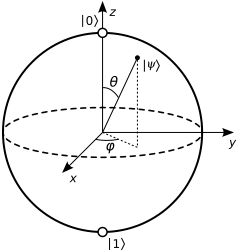
ブロッホ球のZゲートについてどう考えますか？

ブロッホ球でゲートを理解する方法について混乱しています。$Z$

行列と、およびことがわかります。 Z | 0 ⟩ = | 0 ⟩ Z | 1 ⟩ = - | 1 $Z = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}$$Z|0\rangle = |0\rangle$$Z|1\rangle = -|1\rangle$

ここでは、ゲートが軸を中心とした回転であることを説明します。次に、どのように理解すればよいですか？以来南極である、私はと考えるのが自然であると感じ周りの回転軸は何もしません。π Z Z | 1 ⟩ = - | 1 ⟩ | 1 ⟩ π $Z$$\pi$$Z$$Z|1\rangle = -|1\rangle$$|1\rangle$$\pi$$Z$

ブロッホ球について考える方法は、状態の密度行列の観点からです。いずれかに作用するまたは対角密度行列の場合と同様に、何もしません。回転の効果を確認するには、任意の非対角密度行列をによってどのように変化するかを見てする必要があるのような、。| 0 ⟩ ⟨ 0 | | 1 ⟩ ⟨ 1 | Z | + ⟩ ⟨ + $Z$$|0\rangle\langle 0|$$|1\rangle\langle 1|$$Z$$|+\rangle\langle +|$

- | 1 ⟩ | 1 ⟩ ≡ - | 1 ⟩ ≡ θ - | 1 ⟩ = E I θ | 1 $|1\rangle$とは、グローバルフェーズまで等しいため、ブロッホ球の同じ点に割り当てられます。代数的に：ここで、は「グローバルフェーズまで等しい」を意味します。ようながあることを意味します。$-|1\rangle$$|1\rangle \equiv -|1\rangle$$\equiv$$\theta$$-|1\rangle = e^{i \theta} |1\rangle$

混乱を招くのは、およびであるにもかかわらず、2つの線形結合には当てはまらないことです。例えば、たとえ。$|0\rangle \equiv Z |0\rangle$$|1\rangle \equiv Z |1\rangle$| + ⟩ = $Z |+\rangle \not\equiv Z |+\rangle$$|+\rangle = \frac{1}{\sqrt{2}}|0\rangle + \frac{1}{\sqrt{2}}|1\rangle$

Wikipediaに従って、

$$|\psi\rangle = \cos\left( \frac{\theta}{2} \right) |0 \rangle + e^{i \phi} \sin\left( \frac{\theta}{2} \right) |1 \rangle$$

ここで、とはブロッホ球の角度です。$\theta$$\phi$

極を除いて、表面上のほとんどすべての点（つまり、純粋な状態）は、角度に関して一意の表現を持っています。地球と同じように、南極には明確に定義された経度はありません（どの経度も同じように機能します）。状態では、どの位相も同じことを意味します。「緯度」ここにある、その式にのプラグをしてみましょう：φ θ $|1 \rangle$$\phi$$\theta$$\pi$

=0+EIφ| 1

$$|1\rangle = \cos\left( \frac{\pi}{2} \right) |0 \rangle + e^{i \phi} \sin\left( \frac{\pi}{2} \right) |1 \rangle =$$ $$= 0 + e^{i \phi} |1 \rangle$$

オイラーのアイデンティティに精通している場合は、が複雑な平面での回転として認識されるでしょう。特に、は回転なので、有名な、最終的にに到達します。 Z φ = π 電子I π = - 1 | 1 ⟩ = - | 1 $e^{i \phi}$$Z$$\phi = \pi$$e^{i \pi} = -1$$|1 \rangle = - |1 \rangle$