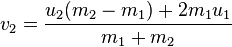ボール対ボールの衝突-検出と処理

Stack Overflowコミュニティの助けを借りて、かなり基本的だが楽しい物理シミュレーターを作成しました。

ボールを発射するには、マウスをクリックしてドラッグします。跳ね返り、最終的には「フロア」で停止します。

追加したい私の次の大きな機能は、ボール同士の衝突です。ボールの動きは、axとyの速度ベクトルに分けられます。私は重力を持っています（各ステップでyベクトルの小さな減少）、私は摩擦を持っています（壁との衝突ごとに両方のベクトルの小さな減少）。ボールは驚くほど現実的な方法で正直に動き回ります。

私の質問には2つの部分があると思います。

1. ボール同士の衝突を検出する最良の方法は何ですか？
   各ボールを反復し、半径が重複しているかどうかを確認するために他のすべてのボールをチェックするO（n ^ 2）ループがあるだけですか？
2. ボール同士の衝突を処理するためにどのような方程式を使用しますか？Physics 101
   2つのボールの速度x / yベクトルにどのように影響しますか？2つのボールが向かう方向は何ですか？これを各ボールにどのように適用しますか？

「壁」の衝突検出とその結果のベクトルの変更の処理は簡単でしたが、ボールとボールの衝突により多くの複雑さが見られます。壁の場合は、適切なxまたはyベクトルの負の値をとるだけで、正しい方向に進みます。ボールの場合はそうは思いません。

いくつかの簡単な説明：簡単にするために、今のところ完全な弾性衝突で大丈夫です。また、すべてのボールは現在同じ質量ですが、将来的に変更する可能性があります。

編集：参考になったリソース

ベクトルを使用した2Dボールの物理学：Trigonometry.pdfのない2次元の衝突
2dボールの衝突検出の例：衝突検出の追加

成功！

ボールの衝突検出と応答がうまく機能しています。

関連コード：

衝突検出：

for (int i = 0; i < ballCount; i++)  
{  
    for (int j = i + 1; j < ballCount; j++)  
    {  
        if (balls[i].colliding(balls[j]))  
        {
            balls[i].resolveCollision(balls[j]);
        }
    }
}

これは、すべてのボール間の衝突をチェックしますが、冗長なチェックをスキップします（ボール1がボール2と衝突するかどうかをチェックする必要がある場合、ボール2がボール1と衝突するかどうかをチェックする必要はありません。また、それ自体との衝突のチェックもスキップします）。

次に、私のballクラスにcolliding（）とresolveCollision（）メソッドがあります：

public boolean colliding(Ball ball)
{
    float xd = position.getX() - ball.position.getX();
    float yd = position.getY() - ball.position.getY();

    float sumRadius = getRadius() + ball.getRadius();
    float sqrRadius = sumRadius * sumRadius;

    float distSqr = (xd * xd) + (yd * yd);

    if (distSqr <= sqrRadius)
    {
        return true;
    }

    return false;
}

public void resolveCollision(Ball ball)
{
    // get the mtd
    Vector2d delta = (position.subtract(ball.position));
    float d = delta.getLength();
    // minimum translation distance to push balls apart after intersecting
    Vector2d mtd = delta.multiply(((getRadius() + ball.getRadius())-d)/d); 


    // resolve intersection --
    // inverse mass quantities
    float im1 = 1 / getMass(); 
    float im2 = 1 / ball.getMass();

    // push-pull them apart based off their mass
    position = position.add(mtd.multiply(im1 / (im1 + im2)));
    ball.position = ball.position.subtract(mtd.multiply(im2 / (im1 + im2)));

    // impact speed
    Vector2d v = (this.velocity.subtract(ball.velocity));
    float vn = v.dot(mtd.normalize());

    // sphere intersecting but moving away from each other already
    if (vn > 0.0f) return;

    // collision impulse
    float i = (-(1.0f + Constants.restitution) * vn) / (im1 + im2);
    Vector2d impulse = mtd.normalize().multiply(i);

    // change in momentum
    this.velocity = this.velocity.add(impulse.multiply(im1));
    ball.velocity = ball.velocity.subtract(impulse.multiply(im2));

}

ソースコード：ボールツーボールコライダーの完全なソース。

この基本的な物理シミュレーターを改善する方法についての提案がある場合は、お知らせください！まだ追加していないことの1つは、角運動量です。これにより、ボールがよりリアルに転がります。他に何か提案はありますか？コメントを残す！

2つのボールが衝突するかどうかを検出するには、中心間の距離が半径の2倍未満かどうかを確認します。ボール間で完全に弾性の衝突を行うには、衝突の方向にある速度の成分のみを考慮する必要があります。他のコンポーネント（衝突に接する）は、両方のボールで同じままです。あるボールから別のボールへの方向を指す単位ベクトルを作成し、ボールの速度ベクトルで内積をとることにより、衝突コンポーネントを取得できます。その後、これらのコンポーネントを1Dの完全弾性衝突方程式に組み込むことができます。

ウィキペディアには、プロセス全体のかなり良い要約があります。任意の質量のボールの場合、新しい速度は次の方程式を使用して計算できます（v1とv2は衝突後の速度であり、u1、u2は以前の速度です）。

ボールの質量が同じ場合、速度が単純に切り替わります。同様のことを実行するために私が書いたコードは次のとおりです。

void Simulation::collide(Storage::Iterator a, Storage::Iterator b)
{
    // Check whether there actually was a collision
    if (a == b)
        return;

    Vector collision = a.position() - b.position();
    double distance = collision.length();
    if (distance == 0.0) {              // hack to avoid div by zero
        collision = Vector(1.0, 0.0);
        distance = 1.0;
    }
    if (distance > 1.0)
        return;

    // Get the components of the velocity vectors which are parallel to the collision.
    // The perpendicular component remains the same for both fish
    collision = collision / distance;
    double aci = a.velocity().dot(collision);
    double bci = b.velocity().dot(collision);

    // Solve for the new velocities using the 1-dimensional elastic collision equations.
    // Turns out it's really simple when the masses are the same.
    double acf = bci;
    double bcf = aci;

    // Replace the collision velocity components with the new ones
    a.velocity() += (acf - aci) * collision;
    b.velocity() += (bcf - bci) * collision;
}

効率については、ライアンフォックスが正解です。領域をセクションに分割し、各セクション内で衝突検出を行うことを検討する必要があります。ボールはセクションの境界で他のボールと衝突する可能性があるため、コードがはるかに複雑になる可能性があることに注意してください。数百個のボールができるまで、効率はおそらく問題になりません。ボーナスポイントについては、異なるセクションで各セクションを実行するか、各セクション内の衝突の処理を分割できます。

ええと、何年も前に私はあなたがここに提示したようなプログラムを作りました。
隠れた問題が1つあります（または多くの場合、見方によって異なります）。

• ボールのスピードが速すぎると、衝突を逃す可能性があります。

また、ほぼ100％の場合、新しい速度は正しくありません。まあ、速度ではなく、位置。新しい速度を正確な場所で正確に計算する必要があります。それ以外の場合は、前の個別のステップから利用できるいくつかの「エラー」量でボールをシフトするだけです。

解決策は明白です。タイムステップを分割する必要があるため、最初に正しい位置にシフトし、次に衝突し、残りの時間シフトします。

この問題を解決するには、スペース分割を使用する必要があります。

バイナリスペースパーティショニング と 四分木について読む

画面を領域に分割し、領域内の衝突のみをチェックするというRyan Foxの提案の明確化として...

たとえば、プレイエリアを四角形のグリッドに分割し（これは任意に1辺の長さが1ユニットであると言います）、各グリッドの四角形内の衝突をチェックします。

それは絶対に正しい解決策です。（別のポスターが指摘しているように）それに関する唯一の問題は、境界を越えた衝突が問題であることです。

これに対する解決策は、最初のグリッドに対して0.5単位の垂直および水平オフセットで2番目のグリッドをオーバーレイすることです。

次に、最初のグリッドの境界を越える（したがって検出されない）衝突はすべて、2番目のグリッドのグリッド内に収まります。すでに処理した衝突を追跡している限り（一部が重複している可能性があるため）、エッジケースの処理について心配する必要はありません。すべての衝突は、グリッドの1つのグリッド内にあります。

衝突チェックの数を減らす良い方法は、画面をいくつかのセクションに分割することです。次に、各ボールを同じセクションのボールとのみ比較します。

私が最適化するためにここに見たものの1つ。

距離が半径の合計である場合にボールがヒットすることには同意しますが、実際にこの距離を計算することはできません。むしろ、それが正方形であることを計算し、それをその方法で処理します。その高価な平方根演算の理由はありません。

また、衝突を見つけたら、衝突がなくなるまで衝突を評価し続ける必要があります。問題は、最初のものが他の人を引き起こし、正確な画像を取得する前に解決する必要があることです。ボールがエッジでボールに当たった場合はどうなるでしょうか？2番目のボールはエッジに当たり、すぐに最初のボールに跳ね返ります。コーナーでボールの山にぶつかった場合、次のサイクルを繰り返す前に解決する必要があるかなりの数の衝突が発生する可能性があります。

O（n ^ 2）に関しては、失敗したものを拒否するコストを最小限に抑えることができます。

1）動いていないボールは何もヒットしません。適度な数のボールが床に転がっている場合、これは多くのテストを節約できます。（静止したボールに何かが当たったかどうかを確認する必要があることに注意してください。）

2）やりがいのあること：画面をいくつかのゾーンに分割しますが、線はぼやけているはずです。ゾーンの端にあるボールは、関連するすべての（4つである可能性があります）ゾーンにあるものとしてリストされます。私は4x4グリッドを使用し、ゾーンをビットとして保存します。2つのボールゾーンのゾーンのANDがゼロを返した場合、テストは終了です。

3）すでに述べたように、平方根を実行しないでください。

2Dでの衝突検出と応答に関する情報が記載された優れたページを見つけました。

http://www.metanetsoftware.com/technique.html

彼らはそれが学問の観点からどのように行われるかを説明しようとします。まず、単純なオブジェクト間の衝突検出から始まり、衝突応答とその拡大方法に移ります。

編集：リンクを更新

これには2つの簡単な方法があります。ジェイはボールの中心からチェックする正確な方法をカバーしました。

より簡単な方法は、長方形のバウンディングボックスを使用し、ボックスのサイズをボールのサイズの80％に設定して、衝突をかなりよくシミュレートすることです。

メソッドをボールクラスに追加します。

public Rectangle getBoundingRect()
{
   int ballHeight = (int)Ball.Height * 0.80f;
   int ballWidth = (int)Ball.Width * 0.80f;
   int x = Ball.X - ballWidth / 2;
   int y = Ball.Y - ballHeight / 2;

   return new Rectangle(x,y,ballHeight,ballWidth);
}

次に、ループで：

// Checks every ball against every other ball. 
// For best results, split it into quadrants like Ryan suggested. 
// I didn't do that for simplicity here.
for (int i = 0; i < balls.count; i++)
{
    Rectangle r1 = balls[i].getBoundingRect();

    for (int k = 0; k < balls.count; k++)
    {

        if (balls[i] != balls[k])
        {
            Rectangle r2 = balls[k].getBoundingRect();

            if (r1.Intersects(r2))
            {
                 // balls[i] collided with balls[k]
            }
        }
    }
}

あちこちでほのめかされていますが、オーバーラップの境界ボックスを比較するなど、最初に計算を高速化することもできます。最初のテストに合格すると、半径ベースのオーバーラップが実行されます。

追加/差分の計算は、境界ボックスの方が半径のすべてのトリガーよりもはるかに高速であり、ほとんどの場合、境界ボックスのテストは衝突の可能性を排除します。しかし、その後trigで再テストすると、求めている正確な結果が得られます。

はい、2つのテストですが、全体的に高速になります。

これKineticModelは、引用されているJavaのアプローチの実装です。

HTML Canvas要素を使用してこのコードをJavaScriptに実装し、毎秒60フレームのすばらしいシミュレーションを生成しました。ランダムな位置と速度のダースボールのコレクションからシミュレーションを開始しました。高い速度では、小さなボールとはるかに大きなボールの間のわずかな衝突により、小さなボールが大きなボールの端にSTICKのように見え、分離する前に大きなボールの周りで最大約90度移動したことがわかりました。（誰か他の人がこの振る舞いを観察したのだろうか？）

計算の一部のログは、これらの場合の最小並進距離が、次のタイムステップで同じボールが衝突するのを防ぐのに十分な大きさではないことを示しました。いくつか実験を行ったところ、相対速度に基づいてMTDをスケールアップすることでこの問題を解決できることがわかりました。

dot_velocity = ball_1.velocity.dot(ball_2.velocity);
mtd_factor = 1. + 0.5 * Math.abs(dot_velocity * Math.sin(collision_angle));
mtd.multplyScalar(mtd_factor);

この修正の前後で、すべての衝突で総運動エネルギーが保存されていることを確認しました。mtd_factorの0.5の値は、衝突後にボールが常に分離することがわかっているおよその最小値でした。

この修正により、システムの正確な物理学に若干のエラーが発生しますが、タイムステップサイズを小さくすることなく、非常に高速なボールをブラウザでシミュレーションできるようになるというトレードオフがあります。