ベイズの定理とは何ですか？

主なアイデア、つまりベイズの定理に関連する概念は何ですか？複雑な数学表記の派生を求めていません。

ベイズの定理は、比較的単純ですが、特定の条件付き確率の計算を可能にする確率理論の基本的な結果です。条件付き確率とは、あるイベントが別のイベントの確率に与える影響を反映した確率です。

簡単に言えば、最も有名な形式では、新しいデータ（P（H | D） ;事後確率と呼ばれる）が与えられた仮説の確率は、次の方程式に等しいと述べています：仮説が与えられた観測データの確率（P（D | H） ;条件付き確率と呼ばれる）、新しい証拠の前に理論が真である確率（P（H） ; Hの事前確率と呼ばれる）を、そのデータを見る確率、期間（P（D）; D）の限界確率と呼ばれます。

正式には、方程式は次のようになります。

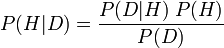
ベイズの定理の重要性は、その適切な使用が確率論の学派間の論争点であることに主に起因しています。主観的なベイジアン（確率を主観的な信念の程度であると解釈する）にとって、ベイズの定理は、主観的な確率の判断を方程式にプラグインして実行することにより、理論のテスト、理論の選択、およびその他の実践の基礎となります。（確率を相対的な頻度を制限するものとして解釈する）頻度主義者にとって、このベイズの定理の使用は虐待であり、代わりに意味のある（非主観的な）事前確率を使用するよう努めています（確率のさらに別の解釈の下で客観的なベイジアンが行うように）。

すみませんが、ここではいくつかの混乱をがあるようです：ベイズの定理はネバーエンディングBayesian-の議論のためにアップしていないFrequentistの議論。これは、コルモゴロフの確率公理と一貫していると仮定すると、両方の考え方に一致する定理です。

もちろん、ベイズの定理はベイジアン統計のコアですが、定理自体は普遍的です。頻度論者とベイジアンの衝突は、主に事前分布を定義できるかどうかに関するものです。

したがって、質問がベイズの定理に関するものである場合（ベイジアン統計ではない場合）：

ベイズの定理は、特定の条件付き確率を計算する方法を定義します。例えば、あなたが知っていることを想像してください：誰かが病気Xを持っていると仮定して、誰かが症状Aを持つ確率p（A | X）; 一般に誰かが病気X p（X）を持っている確率; 一般に誰かが症状A p（A）を持っている確率。これらの3つの情報を使用して、シンポムA p（X | A）がある場合、誰かが疾患Xを持っている確率を計算できます。

ベイズの定理は、条件付き確率を別の条件付き確率P （B | A ）に回転させる方法です。$P(A|B)$$P(B|A)$

いくつかの障害はP （B | Aの意味です。これは、 Aが確実に発生する（または真である）イベントのみを考慮することにより、起こりうるイベントのスペースを削減する方法です。したがって、たとえば、スローされた公平なサイコロが6を示す確率 P （サイコロは 6）ですが、偶数の場合、サイコロが6を着陸する確率は P （サイコロが6 | サイコロの土地も）、1/3です。$P(B|A)$$A$$P(\mbox{dice lands six})$$P(\mbox{dice lands six}|\mbox{dice lands even})$

次のように、ベイズの定理を自分で導き出すことができます。条件付き確率の比率定義から始めます。

$P(B|A) = \frac{P(AB)}{P(A)}$

ここでの同時確率で Aと Bと P （Aは）の周辺確率であり、 A。$P(AB)$$A$$B$$P(A)$$A$

現在、式は参照していないので、この定義も書き留めましょう。$P(A|B)$

$P(A|B) = \frac{P(BA)}{P(B)}$

この作品を作るための小さなトリックは、であることを確認することです（ブール代数がこのすべての下にあるため、 A B = B Aを示すことで真理値表でこれを簡単に証明できます）。次のように書くことができます。$P(AB) = P(BA)$$AB = BA$

$P(A|B) = \frac{P(AB)}{P(B)}$

これを次の式に代入します $P(B|A)$$P(AB)$

$P(AB) = P(A|B)P(B)$

そしてちょっとプレスト：

$P(B|A) = \frac{P(A|B)P(B)}{P(A)}$

ポイントは、このように条件付き確率を回転させるには何であるか、誰かが、彼らが症状を持っていることを所定の疾患を有する確率を推測しようとしているの一般的な例を考えるためとして、すなわち、私たちは知っている、彼らが症状を持っていること-私達はちょうどすることができますそれを参照してください-しかし、私たちは彼らが病気にかかっているかどうかを確信できず、それを推測する必要があります。数式から始めて、やり直します。

$P(\mbox{disease}|\mbox{symptom}) = \frac{P(\mbox{symptom}|\mbox{disease})P(\mbox{disease})}{P(\mbox{symptom})}$

そのためには、症状の事前確率、病気の事前確率（つまり、症状と病気の頻度または頻度）を知る必要があります。病気（例：高価で時間のかかる実験室テストによる）。

複数の病気や症状がある場合など、これよりもはるかに複雑になる可能性がありますが、考え方は同じです。さらに一般的には、原因（病気など）と効果（症状など）の関係の確率理論があり、後方に推論する必要がある場合（たとえば、希望する症状が見られる場合）、ベイズの定理がしばしば登場します。基礎疾患を推測するため）。

統計学には2つの主要な考え方があります。頻度主義者とベイジアンです。

ベイズの定理は後者と関係があり、理論が真実である確率が新しい証拠によってどのように影響を受けるかを理解する方法として見ることができます。これは条件付き確率として知られています。あなたが見たいかもしれませんこれて、数学を理解することができます。

非常に直感的な洞察を提供させてください。コインを10回投げると、8つの頭と2つの尾が得られるとします。あなたの頭に浮かぶ疑問は、このコインが頭に向かって偏っているかどうかです。

今、あなたが従来の定義または確率の頻繁なアプローチで行くならば、あなたはコインが公平であり、これは例外的な出来事であると言うかもしれません。したがって、次のトスを得る可能性も50％であると結論付けます。

しかし、あなたがベイジアンだとします。あなたは実際にあなたが非常に多くの頭を持っているので、コインは頭側に偏っていると思うでしょう。この可能性のあるバイアスを計算する方法があります。あなたはそれらを計算し、次にコインを投げるとき、あなたは間違いなく頭を呼ぶでしょう。

したがって、ベイジアン確率は、観察したデータに基づいて開発した信念に関するものです。それが十分に簡単だったことを願っています。

ベイズの定理は、確率と尤度という2つのアイデアに関連しています。確率は言う：このモデルを考えると、これらは結果です。だから：公平なコインを与えられれば、私は50％の確率で頭を獲得するでしょう。可能性は言う：これらの結果を考えると、これは我々がモデルについて言えることです。したがって、コインを100回投げて88個のヘッドを取得した場合（前の例で取り上げてより極端にするため）、公正なコインモデルが正しい可能性はそれほど高くありません。

ベイズの定理を説明するために使用される標準的な例の1つは、病気のテストのアイデアです：人口の10000人に1人が持っている病気に対して95％正確なテストを行い、テストが陽性の場合、チャンスは何ですかあなたは病気にかかっている？

素朴な答えは95％ですが、これは10000人中9999人のテストの5％が偽陽性になるという問題を無視しています。したがって、この病気にかかる確率は95％をはるかに下回ります。

「あいまいなチャンス」というあいまいなフレーズの使用は意図的です。確率/尤度言語を使用するには、テストが正確である確率は95％ですが、知りたいのは、あなたが病気にかかっている可能性です。

やや外れたトピック：ベイズの定理がすべての教科書で解決するために使用されるもう1つの古典的な例は、モンティホールの問題です：あなたはクイズ番組に出ています。3つのドアの1つに賞品があります。ドアを選択します。ホストはドア3を開いて賞品を公開しません。機会があればドア2に変更すべきですか？

私は質問の言い回しが好きです（以下の参照のおかげです）：あなたはクイズ番組に参加しています。100万個のドアの1つに賞品があります。ドアを選択します。主催者はドア104632を除く他のすべてのドアを開いて賞品を公開しません。ドア104632に変更する必要がありますか？

ベイズの定理をベイズの観点から非常に論じている私のお気に入りの本は、デイビッドJCマッケイの「情報理論、推論、学習アルゴリズム」です。これは、ケンブリッジ大学出版局の書籍、ISBN-13：9780521642989です。私の答えは、この本で行われた種類の議論の蒸留です。（通常の規則が適用されます。著者と提携関係はありません。本が好きです）。

最も明白な形のベイズ定理は、単に2つのことを言い換えたものです。

1. 結合確率は、引数対称です。$P(HD|I)=P(DH|I)$
2. $P(HD|I)=P(H|I)P(D|HI)$

そのため、対称性を使用して：

$P(D|I) \neq 0$$P(D|I)$

これですか？こんなに簡単なものをどうしてこんなにすごいものにできるのでしょうか？ほとんどのものと同様に、「目的地よりも重要な旅」です。ベイズの定理は、それにつながる議論のために揺れ動きます。

$P(H|I)=1-P(\overline{H}|I)$、一貫性のある推論の公理に基づいて演繹的ロジックを使用して導出することができます。

演ductive論理の「ルール」は、「AがBを意味する」という関係がある場合、「Not Bは非Aを意味する」ということです。したがって、「一貫性のある推論はベイズの定理を暗示しています」。これは、「ベイズの定理が一貫性のない推論を意味する」ことを意味します。つまり、結果が事前確率と尤度のベイジアン結果と等しくない場合、一貫性のない推論になります。

この結果はコックスの定理と呼ばれ、1940年代の「推定推論の代数」で証明されました。より最近の派生はProability理論で与えられます：科学の論理。

Kevin MurphyのBayes Theoremの紹介http://www.cs.ubc.ca/~murphyk/Bayes/bayesrule.htmlが本当に好きです

ここでの引用はエコノミストの記事からです：

http://www.cs.ubc.ca/~murphyk/Bayes/economist.html

ベイジアンアプローチの本質は、新しい証拠に照らして既存の信念をどのように変更すべきかを説明する数学的規則を提供することです。つまり、科学者は新しいデータを既存の知識や専門知識と組み合わせることができます。規範的な例は、早産の新生児が彼の最初の日没を観察し、太陽が再び昇るかどうか疑問に思っていることを想像することです。彼は両方の可能な結果に等しい事前確率を割り当て、1つの白い大理石と1つの黒い大理石をバッグに入れることでこれを表します。翌日、太陽が昇ると、子供は別の白い大理石をバッグに入れます。したがって、バッグからランダムに摘み取られた大理石が白になる確率（つまり、将来の日の出に対する子供の信念の程度）は、半分から3分の2になりました。翌日の日の出後、子供は別の白い大理石を追加し、確率（したがって信念の程度）は3分の2から4分の3になります。等々。徐々に、太陽が毎朝昇らない可能性が高いという当初の信念が修正され、太陽が常に昇るというほぼ確実性になりました。