PCAプロットのくさびのような形状は何を示していますか？

テキスト分類用のオートエンコーダに関する彼らの論文で、 HintonとSalakhutdinovは2次元LSA（PCAに密接に関連しています）によって生成されるプロットを示しました。

PCAをまったく異なるわずかに高次元のデータに適用すると、同様に見えるプロットが得られました（この場合を除いて、内部構造があるかどうかを本当に知りたかったのです）。

ランダムデータをPCAに入力すると、ディスク状のブロブが得られるため、このくさび状の形状はランダムではありません。それ自体は何か意味がありますか？

変数が正または非負であると仮定すると、エッジのエッジは、データがそれぞれ0または負になるポイントを超えます。このような実際のデータは正しく歪んでいる傾向があるため、分布の下端にある点の密度が高くなり、したがってくさびの「点」の密度が高くなっています。

より一般的には、PCAは単にデータのローテーションであり、これらのデータに対する制約は、一般的に、質問に示されているのと同じ方法で主成分に表示されます。

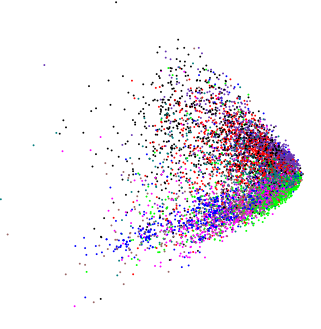
いくつかの対数正規分布変数を使用した例を次に示します。

library("vegan")
set.seed(1)
df <- data.frame(matrix(rlnorm(5*10000), ncol = 5))
plot(rda(df), display = "sites")

最初の2台のPCによって暗黙の回転に応じて、あなたがくさびを見るかもしれないか、あなたは多少異なるバージョンが表示される可能性があり、（使用して3Dでここに示したordirgl()の代わりにplot()）

ここでは、3dで、中央の質量から突き出た複数のスパイクが見られます。

$X_i \sim \mathcal(N)(\mu = 0, \sigma = 1)$

set.seed(1)
df2 <- data.frame(matrix(rnorm(5*10000), ncol = 5))
plot(rda(df2), display = "sites")

そして、一様な正の確率変数の場合、立方体が表示されます

set.seed(1)
df3 <- data.frame(matrix(runif(3*10000), ncol = 3))
plot(rda(df3), display = "sites")

ここでは、説明のために、ランダム変数を3つだけ使用してユニフォームを示しているため、点は3dの立方体を表していることに注意してください。より高い次元/より多くの変数を使用すると、5dハイパーキューブを3dで完全に表すことができないため、明確な「キューブ」形状が多少歪んでしまいます。同様の問題は、表示されている他の例にも影響しますが、これらの例の制約を確認するのは簡単です。

データの場合、線形回帰でこのような変換を使用するのと同じように、PCAの前に変数を対数変換すると、裾が引き込まれ、凝集したデータが引き伸ばされます。

他の形状がPCAプロットに現れる可能性があります。そのような形状の1つは、PCAに保存されているメトリック表現のアーチファクトであり、馬蹄形として知られています。長いまたは支配的な勾配のあるデータ（変数が0から最大に増加し、データの一部に沿って再び0に減少する単一次元に沿って配置されたサンプル）は、このようなアーティファクトを生成することがよく知られています。

ll <- data.frame(Species1 = c(1,2,4,7,8,7,4,2,1,rep(0,10)),
                 Species2 = c(rep(0, 5),1,2,4,7,8,7,4,2,1, rep(0, 5)),
                 Species3 = c(rep(0, 10),1,2,4,7,8,7,4,2,1))
rownames(ll) <- paste0("site", seq_len(NROW(ll)))
matplot(ll, type = "o", col = 1:3, pch = 21:23, bg = 1:3,
        ylab = "Abundance", xlab = "Sites")

これにより、軸の端の点が中央に曲がる極端な馬蹄形が生成されます。