レンズの倍率が1である焦点距離が式と一致しないのはなぜですか？

倍率 Wikipediaのページ、私は次の等式があります。

M = d _i / d _o = f /（​​d _o – f）=（d _i – f）/ f

Mは倍率、fは焦点距離、d _oは被写体からレンズまでの距離、d _iはレンズからセンサーまでの距離です。

したがって、倍率が1の場合、d _i = d _o = 2fが必要です。

私のマクロレンズ（EF 100mm f / 2.8 L IS USMマクロ）では、最小の作動距離（被写体からセンサーまで）は30cmであり、この距離での倍率は1です。式から理解できることから、この距離はd _i + d _o = 4f = 40cm。

だから私は何かが足りないと思います、誰かがどこが間違っているのか説明できますか？

この方程式は、左右対称の単純な単一要素レンズを想定しています。カメラのレンズは、7つの主要な収差（劣化する欠点）を軽減するために、いくつかの個別のガラスレンズ要素を使用して構築されています。あるものは権力において正であり、あるものは負の力を持つ。いくつかは空気で区切られており、いくつかは一緒に接合されています。このアレイは非常に複雑になるため、焦点距離を測定するポイントは、レンズ鏡筒の物理的な中心からずれている可能性があります。

真の望遠設計では、後部節点（測定点）が前方に移動します。このアクションにより、レンズバレルの長さが短くなり、カメラとレンズの保持、使用、および保管が煩雑になります。一部の設計では、後部節が実際にレンズ鏡筒の前方で空中に落ちることがあります。

方程式に示されているように、1（倍率1）では、被写体距離は前方に2焦点距離、バックフォーカスは後方ノードの後方に2焦点距離です。問題は---後部ノードを簡単に見つけることができないことです。ただし、倍率1に達したら、被写体から画像までの距離を測定できます。多くのカメラでは、カメラフレームにシンボル（線で二分された円）が表示されます。イメージプレーンの位置を特定します。

いずれの場合も、被写体と画像の距離を測定し、4で割ります。この割り算により、焦点距離がわかります。2で除算すると、この除算によって後部節点が特定されます。これで、「レンズメーカーの公式」を利用するための準備が整いました。

まず第一に、写真の問題を第一原理に分解するあなたの努力を称賛します。

あなたが観察した不一致は、一般的な過度の単純化に起因します。100 mmレンズは、実際には光学エンジニアが「レンズアセンブリ」と呼んでいるものです。ご存知のように、レンズは複数のレンズ要素で構成されており、連携して動作して、イメージングセンサーで見た画像を形成、改良、および送信します。

100mmレンズアセンブリが単一の100mmレンズエレメントで構成されている場合、大きな歪みが生じ、一度に赤、緑、または青のみに焦点が合う可能性がありますが、リンクした薄いレンズ倍率の式は当てはまります。対象が節点から200mm離れていて、レンズアセンブリが物理的に200mmを超える長さである必要がある場合、倍率は1になります。それでも、これは、薄いレンズの方程式が適切である範囲でのみ厳密に正確になります（ここでは特に適切ではありません）。適切な答えは、レンズメーカーの方程式の導出から得られます。

アセンブリと薄いレンズの違いの当然の結果は、二点の節点です。薄いレンズは、前面および背面節点の両方のための単一の場所を有します。両方とも、入射瞳と同じ場所に配置されています。これがレンズアセンブリに当てはまる場合は、レンズを自由にすることができます。被写体やセンサーへの視差のないレンズの開口部の周りの回転によって。100mmマクロでこれを試した場合、あなたはそれが真実ではないことに気付くでしょう。厚いレンズには2つの節点があり、それらの正味インデックスが0の場合にのみ配置されます。つまり、焦点距離はありません。レンズアセンブリは、仮想レンズが頂点、相対焦点距離、入射瞳、および（大幅に）節点がレンズアセンブリと同じになるように、2つの理想化されたインデックスを持つ仮想厚いレンズで近似できます。

追加のクレジットとして、複合レンズの説明をチェックして、レンズの焦点距離のどの組み合わせが、あなたが説明した状況を生み出すかを推測することができます。注意：「望遠鏡の倍率」。これは本質的にレンズ設計者が行うことです。

詳細については、さまざまなタイプの写真レンズのデザインをチェックしてください

レンズの節点を移動することに加えて焦点距離を変更することにより、ほとんどの固定焦点距離レンズフォーカス。カメラに近いオブジェクトに焦点を合わせるために、レンズは焦点距離を短くします。「100 mm」と指定されたレンズは、通常「無限遠に焦点を合わせた場合は100 mm」ですが、近くの物体に焦点を合わせた場合は必ずしもそうではありません。

単位倍率で被写体と画像の距離が40 cmにならない理由は2つあります。

1. レンズの焦点距離が100 mmでない可能性があります
2. 主平面間の距離はゼロにならない場合があります。

これらの理由のどれが最も重要であるかは、レンズの光学設計に関する詳細な情報なしではわかりません。

焦点距離

レンズ自体に記載されている値「100 mm」は、公称焦点距離であり、通常、レンズが無限遠に焦点を合わせたときの実際の焦点距離の丸められた値です。

通常「ユニットフォーカシング」レンズと呼ばれる一部のレンズは、光学アセンブリ全体を動かすことによって焦点を達成します。これらのレンズには、焦点距離が変化しない焦点距離があります。ただし、ほとんどすべての最新のマクロレンズを含む多くの複雑なレンズには、ある種の「近距離補正」（ニコン用語では）があります。焦点を合わせると光学式が変化するため、収差をより適切に補正できます。これらのレンズには、焦点を合わせると変化する焦点距離があります。

これらの2つの事実：公称焦点距離の丸めと、焦点を合わせるときに変化するという事実は、レンズの実際の焦点距離が単位倍率で何であるかがわからないことを意味します。

主平面

あなたが引用しているウィキペディアのページでは、d _oとd _iをレンズからオブジェクト（または画像）までの距離として定義していますが、これらの定義は特に薄いレンズに関するセクションに表示されています。あなたのレンズは厚い複合レンズであり、これは公式の適用性の問題を引き起こします。

薄いレンズの近似はこの状況では適用できないことがわかります。ただし、厚いレンズモデルのコンテキストで解釈した場合、式は引き続き有効です。このモデルでは、薄いレンズの平面が「主平面」と呼ばれる2つの平面に置き換えられています。

• 「フロント」（または「プライマリ」または「オブジェクト側」）の主平面は、オブジェクト空間の距離を測定するために使用されます
• 「後方」（または「二次」、または「画像側」）の主平面は、画像空間の距離を測定するために使用されます

これらは、単位倍率の共役面です。下の図（ソース）では、これらはH ₁、N ₁およびH ₂、N _2を通過する垂直面です。

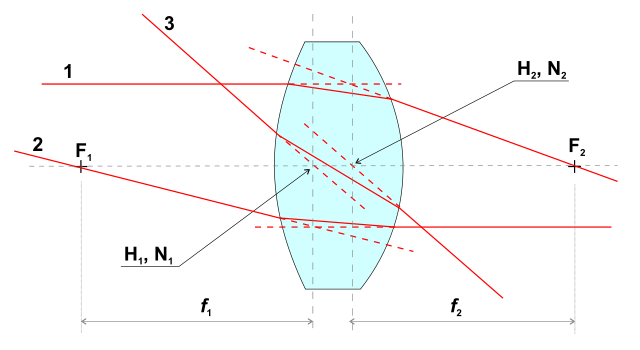
光学系をその基点（上記のF _i、H _i、N _i）で説明するこの方法は、複合レンズにも適用できることに注意してください 。たとえば、両方の主平面（N _iおよびN _oを通る垂直平面）が左端の要素の左側にある望遠レンズ（source）のこの古い図を参照してください。

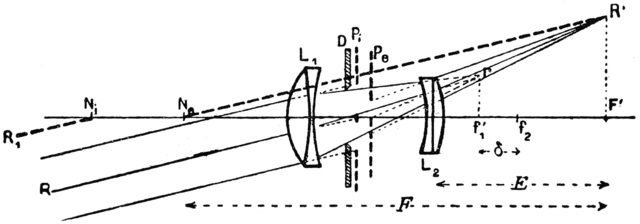
したがって、次のように定義した場合、式は引き続き有効です。

• d _o対象から主要な主平面までの距離
• d _iは二次主平面から画像までの距離

これにより、被写体と画像の距離は次のようになります。

d _o + e + d _i = 4f + e

単位倍率で、ここでeは主平面間の（おそらく負の）距離です。薄いレンズの近似は基本的に主平面が一致している（e = 0）と述べていますが、これはあなたのケースには当てはまりません。

このトピックの詳細については、以下をご覧ください。

• 主飛行機に関するこの短いビデオ
• 厚いレンズに関するこれらの講義ノート

薄いレンズの誤解

この回答は主に、一般的な誤解を明確にするために書いたものです。これは、あなたが受け入れたものも含めて、ここでの回答の一部に表示されます。写真レンズは薄いレンズに相当するということです。

ほとんどの写真の状況（基本的にすべての非マクロ状況）では、被写体からレンズまでの距離は、レンズ自体の特徴的な距離よりもはるかに大きいことがわかります。このような状況では、被写体までの距離を測定するためにどの基準点を使用するかは重要ではありません。その場合、主平面を分離する距離を忘れて、後部の主平面だけが重要なものであると考えると便利です。これは、e = 0を設定することと同じです。これは、基本的に薄いレンズの近似です。

主平面、主点または節点、オブジェクト空間、画像空間などの概念を理解する必要がないため、この近似に固執すると、光学系の学習がはるかに簡単になります。それを考慮して：

• 近似は、ほとんどの（マクロ以外の）目的には十分です
• あなたはレンズを設計するつもりはなく、優れた写真家になるために光学の専門知識を必要としないので、光学に関する知識は定性的なレベルの写真家にのみ役立ちます

薄いレンズが写真家に最も一般的に教えられているモデルであることは理解できます。それでも、マクロ距離で複雑な厚いレンズを扱うと、近似が壊れます。焦点距離が被写体と画像の距離の4分の1であるという答えは、この誤解が人々が間違った答えを投稿する原因となることを示しています。

作動距離はレンズ前面から被写体までの距離です。EF 100mm f / 2.8 L IS USMマクロレンズの場合、最小焦点距離（MFD）/全倍率での作動距離は約133mmです。

焦点距離は、被写体から画像平面（フィルムまたはセンサー）まで測定されます。EF 100mm f / 2.8 L IS USMマクロレンズの場合、フル倍率/ MFDでの焦点距離は300mmです。

ほとんどのレンズの焦点距離は、レンズが無限遠に焦点を合わせたときに測定されます（次に、最も近い「標準」の焦点距離に丸められます）。焦点距離が短くなると、レンズによって提供される画角がしばしば変化します。これは集中呼吸として知られているものです。EF 100mm f / 2.8 L IS USMマクロの300mm MFDは、1：1の倍率での有効焦点距離が約75mmであることを示しています。これは、90〜105mmの範囲の焦点距離を持つマクロレンズではかなり一般的です。たとえば、タムロン90mm f / 2.8 Di VC USDマクロ（F017）も、MFDが1：1で300mmです。

さらに、複合レンズの焦点距離は、同じ量の倍率を提供するために単一のレンズが必要とする焦点距離から概算されます。複合レンズは、通常はグループで配置された複数のレンズのシステムであり、1つのレンズとして機能します。交換レンズカメラシステム用のほとんどすべての市販のレンズは複合レンズです。EF 100mm f / 2.8 L ISマクロには、12個のグループに配置された15個のレンズエレメントがあります。

レトロフォーカス設計のほとんどの広角レンズの場合、この理論上の単純な単一レンズポイントは、レンズの前面のかなり後ろにあります。望遠レンズの場合、このポイントは、定義上、レンズの前にあります。

300mmの最短焦点距離（MFD）で焦点を合わせると、EF 100mm f / 2.8 L IS USMマクロの前面はセンサーの前面で約168mmになります。しかし、MFDのレンズによって提供される視野と倍率により、その焦点距離では事実上75mmレンズになります。これは、1：1の倍率では、単純な75mmレンズがセンサーの前150mmにある必要があります（これにより、被写体から150mm離れたところにも配置されます）。これにより、MFDに焦点を合わせたときに、EF 100mm f / 2.8マクロの有効中心点がレンズの前面の約18mm後ろに配置されます。

だから私は何かが足りないと思います、誰かがどこが間違っているのか説明できますか？

問題のような式を適用する場合、MFDに焦点を合わせるときのレンズの焦点距離には75mmを使用する必要があります。