この問題はO(polylog(b))で解決できます。
f(d, n)n以下の合計桁数を持つ、最大d桁の10進数の整数の数と定義します。この関数は次の式で与えられることがわかります。

より簡単なものから始めて、この関数を導こう。
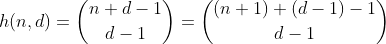
関数hは、n + 1個の異なる要素を含むマルチセットからd-1個の要素を選択する方法の数をカウントします。これは、nをd個のビンに分割する方法の数でもあります。これは、n個の周りにd-1フェンスを構築し、各分離されたセクションを合計することで簡単に見ることができます。n = 2、d = 3 'の例:
3-choose-2 fences number
-----------------------------------
11 ||11 002
12 |1|1 011
13 |11| 020
22 1||1 101
23 1|1| 110
33 11|| 200
したがって、hはnとd桁の桁合計を持つすべての数値をカウントします。ただし、数字は0〜9に制限されているため、nが10未満の場合にのみ機能します。これを10〜19の値に修正するには、9より大きい数の1つのビンを持つパーティションの数を減算する必要があります。これをオーバーフロービンと呼びます。
この項は、次の方法でhを再利用することで計算できます。n-10をパーティション分割する方法の数をカウントしてから、10を入れるビンの1つを選択すると、1つのオーバーフロービンを持つパーティションの数になります。結果は次の予備関数です。
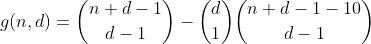
n-20のパーティション分割のすべての方法をカウントし、10を入れる2つのビンを選択して、オーバーフローした2つのビンを含むパーティションの数をカウントすることにより、n以下29のこの方法を続けます。
ただし、この時点では、前の用語で2つのオーバーフローしたビンを持つパーティションをすでにカウントしているため、注意する必要があります。それだけでなく、実際に2回カウントしました。例を使用して、合計21のパーティション(10,0,11)を見てみましょう。前の項では、10を減算し、残りの11のすべてのパーティションを計算し、10を3つのビンのいずれかに入れました。ただし、この特定のパーティションには、次の2つの方法のいずれかで到達できます。
(10, 0, 1) => (10, 0, 11)
(0, 0, 11) => (10, 0, 11)
これらのパーティションも最初の用語で1回カウントしたので、2つのオーバーフローしたビンを持つパーティションの合計カウントは1-2 = -1になるため、次の用語を追加してもう一度カウントする必要があります。
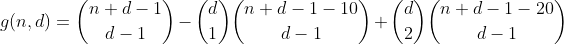
これについてもう少し考えてみると、特定の用語で特定のオーバーフロービン数を持つパーティションがカウントされる回数は、次の表で表現できることがすぐにわかります(列iは用語iを表し、行jパーティションはjオーバーフローしますビン)。
1 0 0 0 0 0 . .
1 1 0 0 0 0 . .
1 2 1 0 0 0 . .
1 4 6 4 1 0 . .
. . . . . .
. . . . . .
はい、パスカルの三角形です。関心のある唯一のカウントは、最初の行/列のカウント、つまり、オーバーフローしたビンがゼロのパーティションの数です。そして、最初の行を除くすべての行の交互の合計が0(たとえば、1-4 + 6-4 + 1 = 0)であるため、これを削除して最後から2番目の式に到達します。
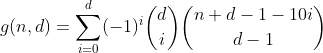
この関数は、数字の合計がnであるd桁の数値をすべてカウントします。
では、nより小さいdigit-sumの数字はどうでしょうか?二項式に標準的な再帰と帰納的引数を使用して、
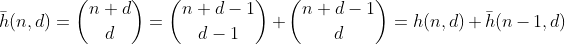
最大nの数字の合計を持つパーティションの数をカウントします。そして、これからgと同じ引数を使用してfを導出できます。
この式を使用すると、たとえば8000から8999までの間隔で重い数字の数を見つけることができ1000 - f(3, 20)ます。この間隔には1000個の数字があるため、数字の合計が28以下の数字の数を減算する必要があります一方、最初の数字が既に数字の合計に8を与えていることをカウントします。
より複雑な例として、間隔1234..5678の重い数字の数を見てみましょう。最初に1のステップで1234から1240に移動します。次に、10のステップで1240から1300に移動します。上記の式は、このような各間隔での重い数の数を示しています。
1240..1249: 10 - f(1, 28 - (1+2+4))
1250..1259: 10 - f(1, 28 - (1+2+5))
1260..1269: 10 - f(1, 28 - (1+2+6))
1270..1279: 10 - f(1, 28 - (1+2+7))
1280..1289: 10 - f(1, 28 - (1+2+8))
1290..1299: 10 - f(1, 28 - (1+2+9))
次に、100のステップで1300から2000に進みます。
1300..1399: 100 - f(2, 28 - (1+3))
1400..1499: 100 - f(2, 28 - (1+4))
1500..1599: 100 - f(2, 28 - (1+5))
1600..1699: 100 - f(2, 28 - (1+6))
1700..1799: 100 - f(2, 28 - (1+7))
1800..1899: 100 - f(2, 28 - (1+8))
1900..1999: 100 - f(2, 28 - (1+9))
2000から5000まで1000のステップで:
2000..2999: 1000 - f(3, 28 - 2)
3000..3999: 1000 - f(3, 28 - 3)
4000..4999: 1000 - f(3, 28 - 4)
ここで、ステップサイズを再度小さくする必要があります。100のステップで5000から5600、10のステップで5600から5670、最後に1のステップで5670から5678になります。
Python実装の例(その間にわずかな最適化とテストを受けました):
def binomial(n, k):
if k < 0 or k > n:
return 0
result = 1
for i in range(k):
result *= n - i
result //= i + 1
return result
binomial_lut = [
[1],
[1, -1],
[1, -2, 1],
[1, -3, 3, -1],
[1, -4, 6, -4, 1],
[1, -5, 10, -10, 5, -1],
[1, -6, 15, -20, 15, -6, 1],
[1, -7, 21, -35, 35, -21, 7, -1],
[1, -8, 28, -56, 70, -56, 28, -8, 1],
[1, -9, 36, -84, 126, -126, 84, -36, 9, -1]]
def f(d, n):
return sum(binomial_lut[d][i] * binomial(n + d - 10*i, d)
for i in range(d + 1))
def digits(i):
d = map(int, str(i))
d.reverse()
return d
def heavy(a, b):
b += 1
a_digits = digits(a)
b_digits = digits(b)
a_digits = a_digits + [0] * (len(b_digits) - len(a_digits))
max_digits = next(i for i in range(len(a_digits) - 1, -1, -1)
if a_digits[i] != b_digits[i])
a_digits = digits(a)
count = 0
digit = 0
while digit < max_digits:
while a_digits[digit] == 0:
digit += 1
inc = 10 ** digit
for i in range(10 - a_digits[digit]):
if a + inc > b:
break
count += inc - f(digit, 7 * len(a_digits) - sum(a_digits))
a += inc
a_digits = digits(a)
while a < b:
while digit and a_digits[digit] == b_digits[digit]:
digit -= 1
inc = 10 ** digit
for i in range(b_digits[digit] - a_digits[digit]):
count += inc - f(digit, 7 * len(a_digits) - sum(a_digits))
a += inc
a_digits = digits(a)
return count
編集:コードを最適化されたバージョンに置き換えました(元のコードよりもevenいように見えます)。また、私がそこにいた間にいくつかのコーナーケースを修正しました。 heavy(1234, 100000000)私のマシンでは約1ミリ秒かかります。
